The Coq language

As mentioned on the Inria website, Coq is a formal proof management system. It provides a formal language to write mathematical definitions, executable algorithms and theorems together with an environment for semi-interactive development of machine-checked proofs. Typical applications include the certification of properties of programming languages (e.g. the CompCert compiler certification project, the Verified Software Toolchain for verification of C programs, or the Iris framework for concurrent separation logic), the formalization of mathematics (e.g. the full formalization of the Feit-Thompson theorem, or homotopy type theory), and teaching.

For more information, please read the Coq documentation.

Some syntactical elements of the Coq language

Coq language

• Boolean type definition:

 Inductive  bool : Type :=
     | true
     | false.

• Definition of a function that returns the denial of a Boolean:

Definition negb (b:bool) : bool :=
     match b with
     | true => false
     | false => true
     end.

A few syntactical elements of the Coq language

Here is an example of proof that may be implemented:

test_orb1: (orb true false) = true.

Proof.
simpl. (* ===> true = true *)
reflexivity. (* ===> no more subgoals *)
Qed.

The example above shows that true or false equals true. The first line matches the one that we want to demonstrate. The lines between the Proof and Qed keywords form the proof. All words between Proof and Qed[^2] are called tactics. These are functions that allow us to make our demonstration step by step. All tactics are referenced in the list of Coq tactics. ​

Proof creation using Mi-Cho-Coq

As Coq is a proof software that has its own syntax, the difficulty has been in finding a way to translate the Michelson code into Coq.

Mi-Cho-Coq is the library that allows you to do this. When you wish to prove a smart contract written or compiled down in Michelson, you must use this library and import the code that you wish to formally prove. The syntax to be used at the start of the file containing the proof is as follows:

Require Import Michocoq.macros. Import syntax.
Require Import Michocoq.semantics. Require Import Michocoq.util.
Import error.

For a more technical understanding of the operation of Mi-Cho-Coq, this tutorial can be viewed: ​ ​

Execution of a simple proof using Coq software

We can execute the proof of 'Example test_orb2" (Example keyword below) using the Coq proof assistant.

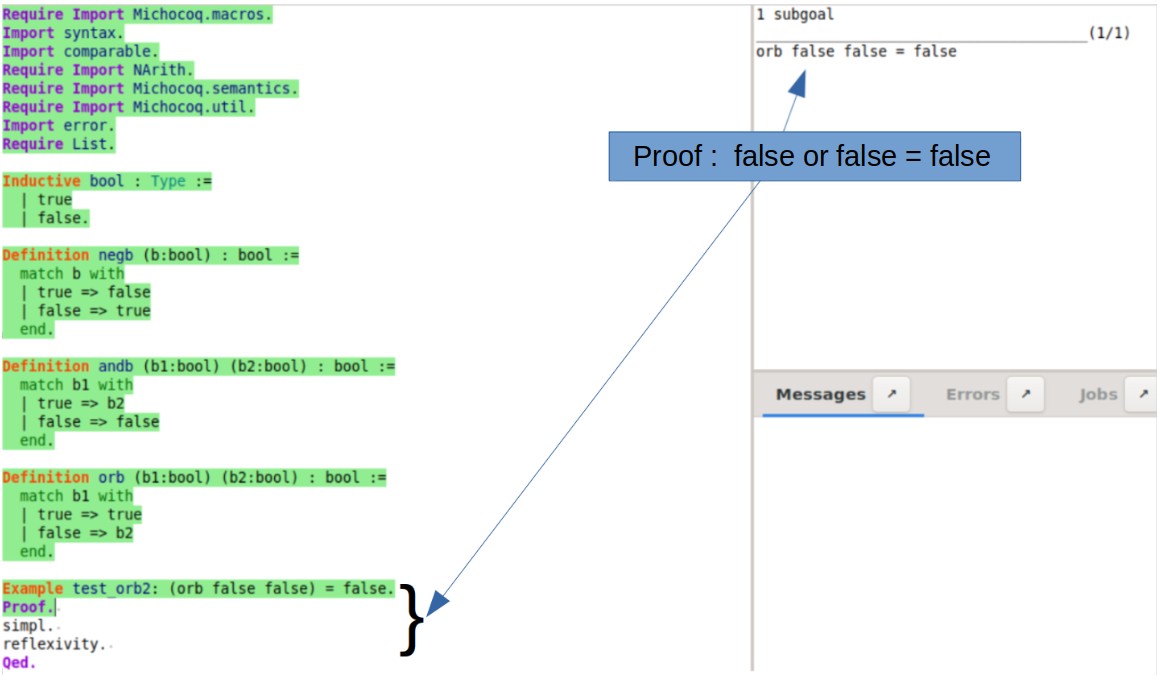
End of proof.